粉末压制理论
- 詳細
- カテゴリ: 钨业知识
- 2017年4月13日(木曜)20:34に公開
- 作者: ruibin
- 参照数: 3654
在粉末冶金中粉末压型是与粉末烧结同样的重要问题。随着粉末冶金技术的应用与发展,粉末成形工艺的研究的活跃,粉末压型理论的研究必须与形势需要相适应。自1923年Walker最先提出在粉末压型时粉末相对体积与压制压力的对数呈线性关系的经验公式以来,许多学者对粉末压型问题进行了一系列的研究。其中最著名的有黄培云压制方程川、 北公夫方程、康诺匹茨基方程和巴尔申方程等。
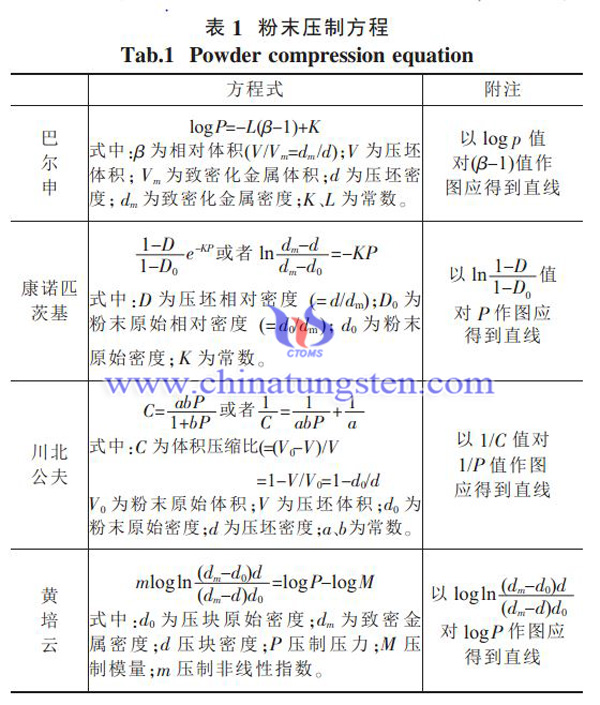
1、巴尔申方程由前苏联粉末冶金学家M.I.O.巴尔申于1938年提出。适用于脆硬性粉末或中等硬度粉末的压制适用于中等压力范围对于塑性较好较高或者较低压力时的则会出现偏差。
2、康诺匹茨基公式表明压制压力与压坯相对密度成直线关系公式在中压及高压范围内应用较好 在很低的压力下出现偏差适用于大多数粉末的压制。此外,由美国人艾西(E.F.Athy)和沙皮罗(I.Shapiro)分别提出的两种压制公式与柯诺皮斯基压制公式属于同一类型的公式。
3、川北公夫公式形式简单没有采用对数关系对低压力范围和软粉末适应较好 大多数粉末压型理论都把粉末体作为弹性体处理并忽略硬化影响 而且还忽略了时间因素等等所以应用范围有限。
4、黄培云压制公式在考虑应变充分弛豫状态下得出了粉末压制的对对数方程 该方程既适合于硬粉也适合于软粉 适用于粉末压制成形 也适用于粉末冷等静压成形 同时还适用于存在模壁摩擦的钢模中的单向压制。与巴尔申、柯诺皮斯基和川北公夫的压制公式相比,黄培云双对数压制方程的直线关系符合最好,其回归直线的相关系数R最接近于1。
| 硬质合金供应商:中钨在线科技有限公司 | 产品详情: http://www.tungsten-carbide.com.cn |
| 电话:0592-5129696 传真:5129797 | 电子邮件:sales@chinatungsten.com |
| 钨钼文库:http://i.chinatungsten.com | 钨钼图片: http://image.chinatungsten.com |
| 钨新闻3G版:http://3g.chinatungsten.com | 钼业新闻: http://news.molybdenum.com.cn |
微博

微信







 sales@chinatungsten.com
sales@chinatungsten.com