压制速率相等原则
- 詳細
- カテゴリ: 钨业知识
- 2017年4月20日(木曜)20:01に公開
- 作者: ruibin
- 参照数: 2204
在压制带台阶的复杂压坯时,除了要考虑各台阶的压缩比相同外,还要考虑到各个台阶区域的压制速度。为了防止粉末在压制过程中的不产生侧向运动,各台阶的压制速度或压制压力满足速率平衡方程或压应力变化率平衡方程,即符合:
Hi/Hi+1=vi/vi+1(1)
式中:Hi---任意高度区的装粉高度;
Vi---任意高度区的压制速度(=dHi/dt)。
或:
dPi/dt/Si=dPi+1/dt/Si+1(2)
式中:dPi/dt---任意高度区的总压力变化速率;
si---任意高度区的正压面积。
以下图为例,若用公式表示,A区中单位时间被压缩掉的体积与原粉末体积之比(压缩速率)为:
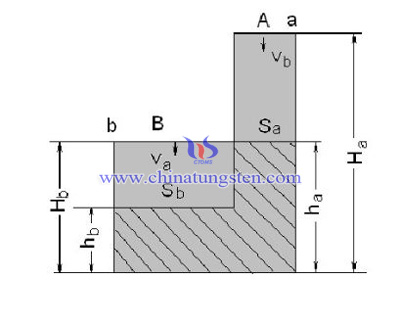
na=(Vo-V)/Vot=(HaSa-haSa)/HaSat=(Ha-ha)/Hat(3)
同理,B区中,单位时间内被压缩的体积与原体积之比为:
nb=(Hb-hb)/Hbt(4)
式中,Vo、V---分别为粉末压缩前、后的体积;
t---压制时间;
Ha、Hb分别为a区、b区粉末在压缩前的高度;
ha、hb分别为a区、b区粉末在压缩后的高度;
Sa、Sb分别为a区、b区的截面积(在压制时为常数);
则(3)式可一般性地改写为:
n=(H-h)/th=v/H(5)
式中,v为压制速度,
H为粉末压制前的高度。
在任何高度区的压制速度都可表为:
vi=niHi
则:vi/vi+1=niHi/ni+1Hi+1(6)
与(1)相比可知,ni=ni+1
因此,压制速率相等原则也可以叙述为压缩速率相等。
| 硬质合金供应商:中钨在线科技有限公司 | 产品详情: http://www.tungsten-carbide.com.cn |
| 电话:0592-5129696 传真:5129797 | 电子邮件:sales@chinatungsten.com |
| 钨钼文库:http://i.chinatungsten.com | 钨钼图片: http://image.chinatungsten.com |
| 钨新闻3G版:http://3g.chinatungsten.com | 钼业新闻: http://news.molybdenum.com.cn |
微博

微信

