硬质合金烧结机制-蒸发凝聚
- 详细资料
- 分类:钨业知识
- 发布于 2017年6月06日 星期二 16:59
- 作者:ruibin
- 点击数:2789
硬质合金烧结过程伴随物质迁移,在高温下,烧结过程中还可能发生物质由颗粒表面向空间蒸发的现象,同样对烧结的致密化和孔隙的变化产生直接的影响。因此,烧结动力也可以从物质蒸发凝聚的角度来研究,即用饱和蒸气压的差表示烧结动力。
利用理想的两球模型,用吉布斯-凯尔文(Gibbs-Kelvin)方程计算出,曲面的饱和蒸气压与平面的饱和蒸气压之差为:
ΔP曲=-PγΩ/kTρ(1)
式中,P--平面的饱和蒸气压;
γ--表面张力;
Ω--单个空位的体积;
k--玻尔兹曼常数;
T--系统温度;
ρ--烧结颈曲率半径。
当粉末颗粒的半径α比烧结颈曲率半径ρ大得多时,可认为球表面蒸气压P对平面蒸气压的差比ΔP曲小得多,可以忽略不计,因此,球表面的蒸气压与颈表面(凹面)蒸气压的差可近似地写成
ΔP=PγΩ/kTρ(2)
蒸气压差使得原子从球表面蒸发,重新再烧结颈凹面凝聚下来,这是蒸发于凝聚物质迁移的模型,蒸发速度与蒸气压差相关。烧结颈长大的速率随ΔP而增大,物质转移即凝聚的速率可用单位面积上、单位时间内凝聚的物质量m表示,可近似地应用南格缪尔公式计算
m=ΔP(M/2πRT)1/2(3)
式中,M--物质的原子量;
R--气体常数。
烧结颈长大速率用颈体积V的增大速率表示时有,
dV/dt=(m/d)A(4)
式中,A--烧结颈曲面面积;
d--粉末的理论密度。
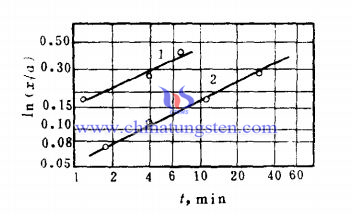
烧结蒸发凝聚动力学方程图片
经过联立计算得,
x3/a=Kt(5)
式中,x--烧结颈半径;
a--颗粒半径;
t--烧结时间;
K--常系数。
从(5)式说明,蒸发与凝聚机构的特征速度方程是烧结颈半径x的三次方与烧结时间t成线性关系。
| 高比重合金供应商:中钨在线科技有限公司 | 产品详情: http://www.tungsten-alloy.com |
| 电话:0592-5129696 传真:5129797 | 电子邮件:sales@chinatungsten.com |
| 钨钼文库:http://i.chinatungsten.com | 钨钼图片: http://image.chinatungsten.com |
| 钨新闻3G版:http://3g.chinatungsten.com | 钼业新闻: http://news.molybdenum.com.cn |
微博

微信





